Sam Moore

PhD Candidate, ME
AI Scientist, Roboticist, Dynamicist
Duke University
sam.a.moore@duke.edu

I am an NSF Graduate Research Fellow in the General Robotics Lab @ Duke University, advised by Dr. Boyuan Chen.

Prior joining the General Robotics Lab, I was a member of the Duke Dynamical Systems Lab advised by Dr. Brian Mann.

As a PhD student, I have worked across AI, robotics, dynamical systems, and control.

I completed my bachelors studies at the University of Kentucky in kinesiology and statistics.

Google Scholar / Linkedin / Github

News

[2024 Nov] I presented at the AAAI FSS for Integrated Computational Approaches for Scientific Discovery.

[2024 Nov] Our work on automated scientific discovery in dynamics was released.

[2023 Jul] Our paper was accepted to the Journal of Sound and Vibration

[2023 Apr] Successfully defended my dissertation proposal

Research

Part of my research centers on developing integrated computational frameworks for scientific discovery in dynamical systems, robotics, and control. I also focus on designing adaptable, whole-body-aware robots that leverage deep learning to achieve robust performance in complex, real-world environments.

	Automated Global Analysis of Experimental Dynamics through Low-Dimensional Linear Embeddings Sam A. Moore , Brian P. Mann, Boyuan Chen Arxiv Preprint paper project page code youtube This work presents an end-to-end approach for discovering hidden stuctures in experimental data from dynamical systems. We simulaneously address challenges in applied dynamical systems due to mathematical modelling, nonlinearity, and high dimensionality through low-dimensional linear embeddings of nonlinear dynamics.
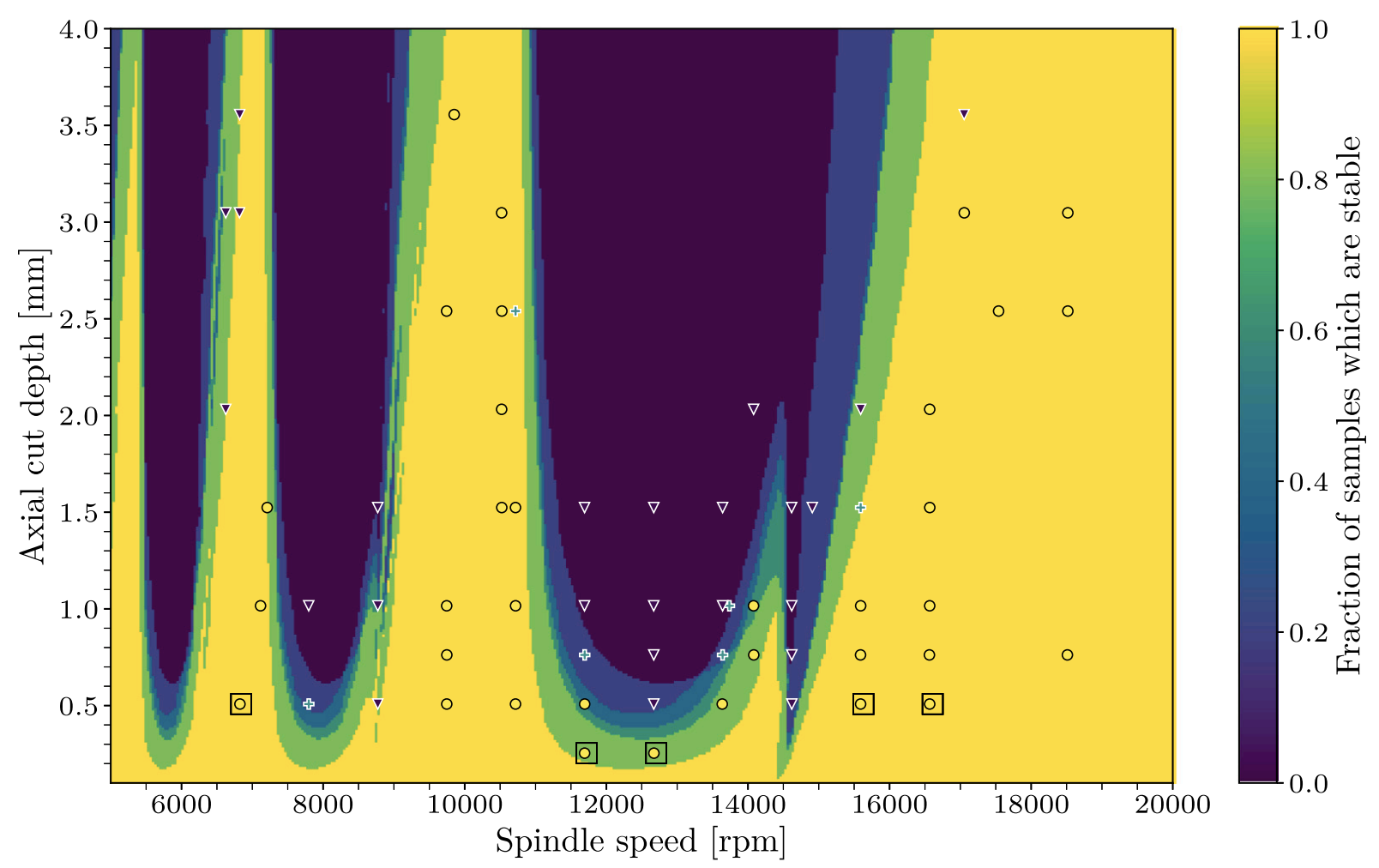
	Stability Prediction via Parameter Estimation from Milling Time Series James D. Turner, Sam A. Moore, Brian P. Mann Journal of Sound and Vibration, 2023 paper This paper introduces an approach to automated milling stability analysis whereby the vibration behavior of a milling tool during cutting is used to directly obtain a bifurcation diagram of the system at real-time rates.
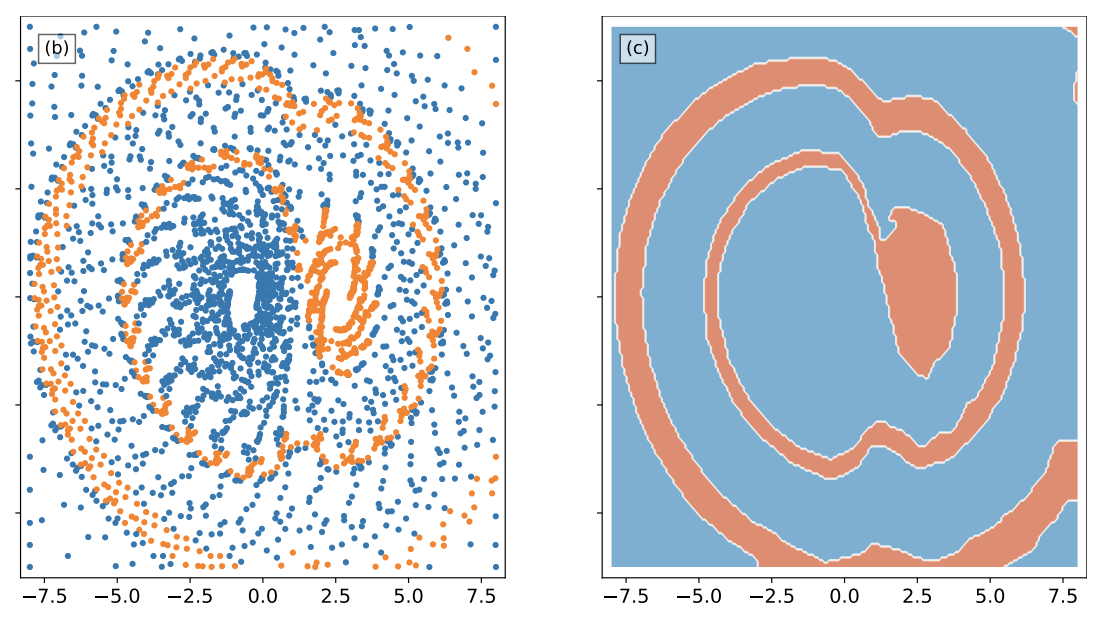
	A Model-Free Sampling Method for Basins of Attraction Using Hybrid Active Learning Xue-She Wang, Sam A. Moore, James D. Turner, Brian P. Mann Communications in Nonlinear Science and Numerical Simulation. 2022 paper project page This work explores hybrid active learning as an efficient method to automatically discover the basins of attraction of dynamical systems.
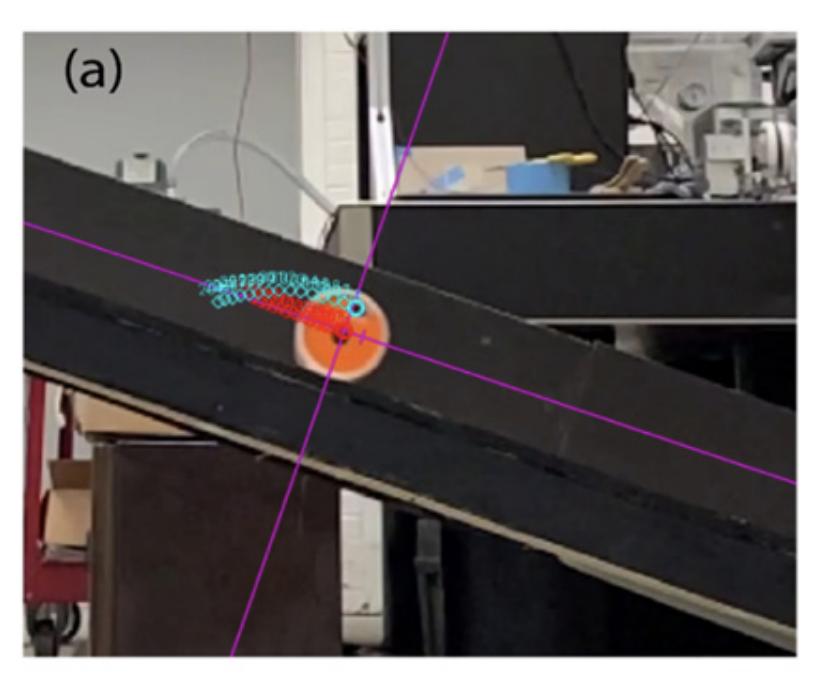
	Supervised Learning for Abrupt Change Detection in a Driven Eccentric Wheel Sam A. Moore, Dean Culver, Brian P. Mann International Modal Analysis Conference, 2021 paper This paper seeks to explore and compare supervised learning methods for phase identification (i.e., roll, slip, and hop) in simulated data from a driven eccentric wheel as a prototypical non-smooth system.
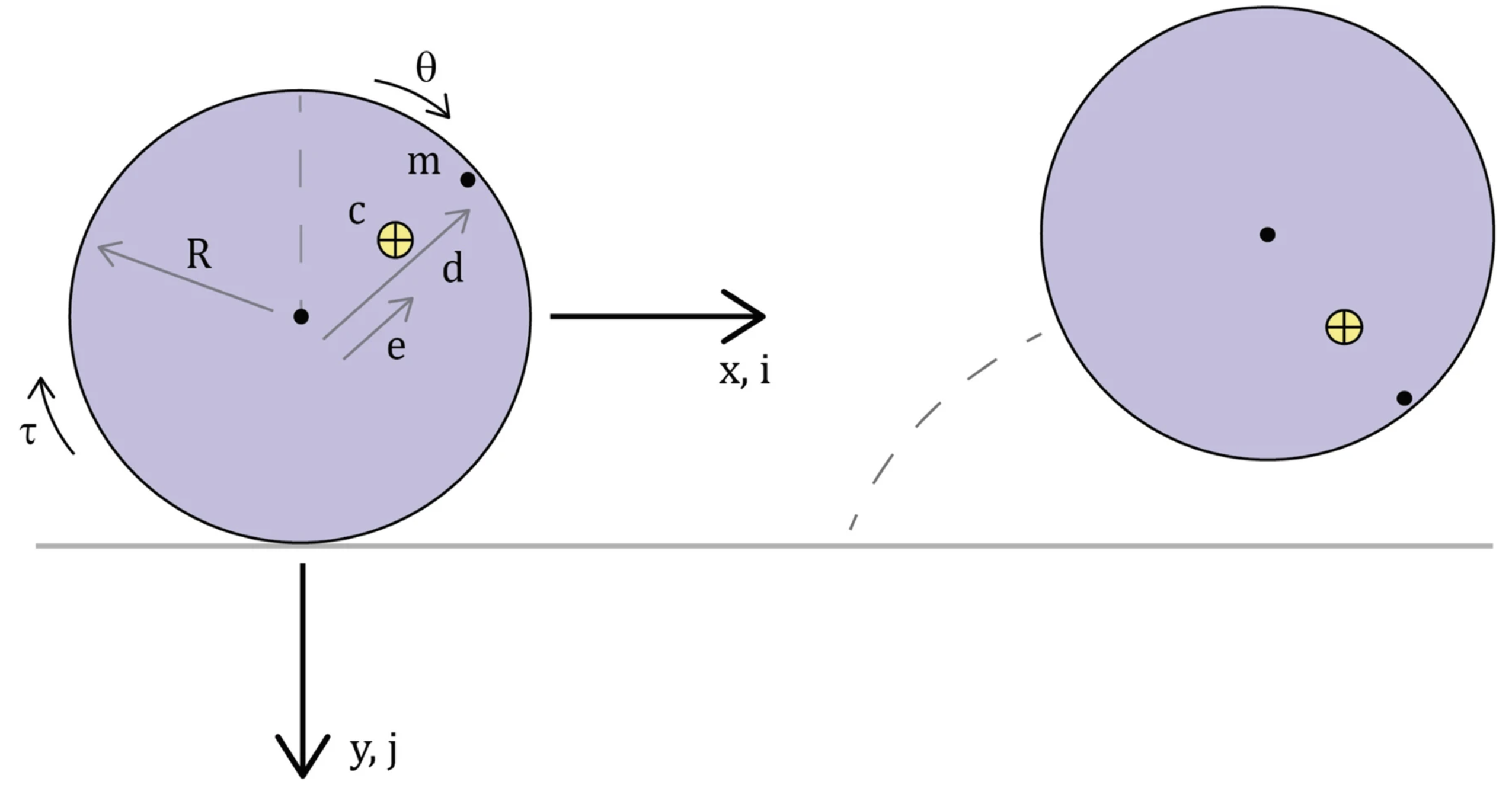
	The Eccentric Disk and Its Eccentric behavior Sam A. Moore, Dean Culver, Brian P. Mann European Journal of Physics, 2021 paper An eccentric disk has a non-constant normal force and therefore has four distinct phases of motion: oscillations about a stable equilibrium, roll without slip, roll with slip, and hop. In this work, the system is analytically modeled using an augmented Lagrangian formulation, solved with numerical integration, and experimentally realized.

Webpage template from Jon Barron